深度学习优化算法——学习总结

文章作者：佚名人气：发表时间：2024-08-26 06:13:28

作为一个深度学习的初学者，从最基础的线性回归、Logistic回归，到更深层次的神经网络分析，在短短的学习历程中，我不止一次地叹服于种种算法在一次次发展进程中迸发出的强大的创新力与生命力。所以，在学习了几种优化算法之后，我想稍稍加以总结，以便日后学习回顾。不当之处，恳请见谅并指出。

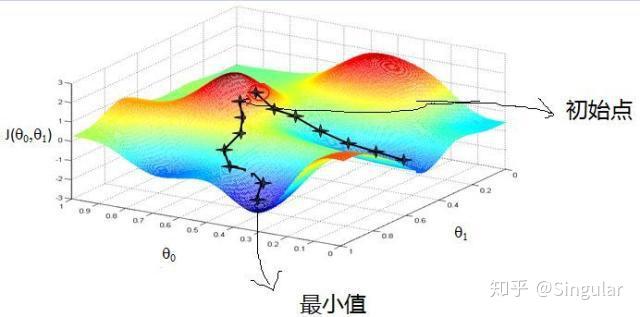
对于给定待优化模型的参数 $\ heta \\in \\mathbb{R}^d$ 和目标函数 $J(\ heta)$ ，梯度下降算法可以通过迭代收敛到目标函数的最小值。（类比于步行下山的场景）

通常可以将梯度下降算法分为三种：

用全部的训练集来进行梯度下降： $\ heta：=\ heta - \\alpha\\frac{1}{m}d\ heta$

其中， $\\alpha$ 为学习率，决定了更新参数的幅度大小；m代表训练集样本数量

算法评价：

从某处开始带入训练集全部数据计算梯度，相对噪声较低，下降幅度较大；
该算法的主要弊端在于每个迭代需要处理大量训练样本，特别是在训练样本数量巨大的时候，单次迭代耗时太长。
如果训练样本不大，batch梯度下降法运行地很好。

每次随机选取一个样本来进行梯度下降: $\ heta:=\ heta-\\alpha d\ heta$

算法评价：

从某一点开始，每次迭代，只对一个样本进行梯度下降，平均来看，它最终会靠近最小值，不过有时候也会方向错误，因此随机梯度下降法是有很多噪声的；
随机梯度下降法永远不会收敛，而是会一直在最小值附近波动，并不会达到最小值并最终停留在此；
虽然通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是，你会失去所有向量化所带来的加速，因为一次性只处理了一个训练样本，效率过于低下。

当样本数量（m）较大时，我们将训练集分割为小一点的子集，称为mini-batch。

假设：m=500万，将 $x^{（1）}-x^{（1000）}$ 取出来作为第一个子训练集，以此类推，共有5000个mini-batch。

每次都用mini-batch来进行梯度下降： $\ heta：=\ heta - \\alpha\\frac{1}{k}d\ heta$

其中，k为mini-batch的大小

算法评价：

一方面，得到了大量向量化，如果mini-batch大小为1000个样本，我们就可以对1000个样本向量化，比一次性处理多个样本快得多；
另一方面，无需等待整个训练集被处理完就可以开始进行后续工作。

所以，综合考量，MBGD算法在多数情况下更优

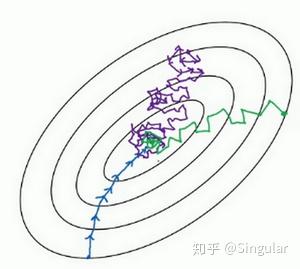
在使用梯度下降算法训练参数时，有时候会下降的非常慢，并且可能会陷入到局部最小值中，在此基础上，引入动量梯度下降算法来加快学习过程，特别是对于高曲率、小但一致的梯度，或者噪声比较大的梯度效果更佳。其主要思想在于积累了之前梯度指数级衰减的移动平均（即前面梯度的指数加权平均）。

在MBGD中加入动量：

On iteration t:

Compute $d\ heta$ on the current mini-batch:

$v_{d\ heta}=\\beta v_{d\ heta}+(1-\\beta)d\ heta$

$\ heta:=\ heta-\\alpha v_{d\ heta}$

其中，t为mimi-batch的数量；超参数 $\\alpha$ 为学习率， $\\beta$ 一般取0.9~0.99 ( $\\beta$ 的值越大，则之前的梯度对现在的方向影响越大)，推荐值为0.9； $v_{d\ heta}$ 的初始值为0。

注：在动量梯度下降算法中，一般不用考虑偏差修正

算法评价：

有效减缓甚至消除了梯度下降中的摆动，大大加快了学习速度。

NAG是在Momentum算法上更进一步的改良——在NAG中，我们通过计算未来位置的梯度，来代替当前位置的梯度，使得动量会在梯度达到最小值之前就开始减小，以此来提高算法的稳定性。

有Momentum算法可知： $\ heta=\ heta-\\alpha(1-\\beta)d\ heta-\\alpha\\beta v_{d\ heta}$

考虑到， $\\alpha d\ heta$ 很小，

所以， $\ heta=\ heta-\\alpha\\beta v_{d\ heta}$ 即为未来权重的计算值

对未来权重计算梯度得到新动量方程： $v_{d\ heta}=\\beta v_{d\ heta}-\\alpha d\ heta$

算法评价：

可以使算法更好的预测未来，提前调整更新速率；
提高了算法得稳定性，使得在收敛时产生较小的震荡。

目前，我只能将自适应算法粗浅地理解为使学习率随训练而改变，使其自动适应学习过程得算法。

经历过向前传播过程后，每个权重都有缓存值，用于反向传播梯度计算。Adagrade算法原理是：如果权重进行了非常大得更新，那么，该权重的缓存值将会增加，学习率将会变小，抑制其更新；反之，学习率将会增大，从而迫使参数进行较大的更新。

On iteration t:

Compute $d\ heta$ on the current mini-batch：

$s_{d\ heta}:=s_{d\ heta}+(d\ heta)^{2}$ (缓存更新公式)

$\ heta:=\ heta+\\frac{\\alpha}{\\sqrt{cache+\\varepsilon}}d\ heta$ (权重更新公式)

其中，分母上的 $\\varepsilon$ 是一个很小的值（通常取 $10^{-8}$ ），确保分母不为零

算法评价：

因为权重的更新幅值会随着迭代次数的增大而减小，所以一般来说AdaGrad算法开始时是激励收敛，后期就是惩罚收敛，速度会越来越慢；
AdaGrad符合训练初期参数离最优比较远（适合大的学习率），训练后期参数离最优较近（适合小的学习率）的客观规律；
针对不同的参数AdaGrad给出不一样的学习速率；
缓存值始终会增加一定的量，使得每个权重的学习率都会降到非常小的值，以至于训练无法再有效进行。

RMSprop算法针对Adagrade算法进行了改进。

On iteration t:

Compute $d\ heta$ on the current mini-batch：

$s_{d\ heta}:=\\beta s_{d\ heta}+(1-\\beta)(d\ heta)^{2}$ (缓存更新公式)

$\ heta:=\ heta+\\frac{\\alpha}{\\sqrt{cache+\\varepsilon}}d\ heta$ (权重更新公式)

算法评价：

RMSProp 算法在AdaGrad的基础上改变梯度积累为指数加权的移动平均，可以更好地应用于应用于非凸函数训练神经网络；
相比于 AdaGrad，使用移动平均引入了一个新的超参数 $\\beta$ ，用来控制移动平均的长度范围；
事实上， RMSProp 已被证明是一种有效且实用的深度神经网络优化算法，目前它是深度学习从业者经常采用的优化方法之一。

除了RMSProp算法以外，另一个常用优化算法AdaDelta算法也针对AdaGrad算法在迭代后期可能较难找到有用解的问题做了改进。但AdaDelta算法没有学习率这一超参数。
AdaDelta算法也像RMSProp算法一样，使用了小批量随机梯度 $d\ heta$ 按元素平方的指数加权移动平均变量 $s_{d\ heta}$ 。在时间步0，它的所有元素被初始化为0.给定超参数 $0\\leq\\rho\\leq1$ (对应RMSprop算法中的 $\\beta$ )，在时间步 $t>0$ ,与RMSprop算法相同：