和以及到底做了什么？
这中间的迭代到底是怎样发生的呢？
从头开始，我们来分别搞懂这三个操作的含义

假设我们已知一个函数：$f(x)=x^3$，我们需要求 $f^{{}^{\prime }}(4)=?$，我们通过口算知道：$f^{{}^{\prime }}(x)=3x^2$,$f^{{}^{\prime }}(4)=3?4^2=48$，那在torch里面应该怎样写呢？

torch里面有自动求导函数，用法代码如下：

输出：

如上所见，利用 $f$Tensor.backward()，可以计算 $f^{{}^{\prime }}(x)$，结果储存在 xTensor.grad 对象里面。

（1）单位tensor 和 类Tensor 和构建函数torch.tensor()

单位 tensor：相当于一种最小的盛放数据容器。我们不可操作
类 Tensor：里面有几个或一个（大多数情况下）单位tensor，还带有其他函数属性，我们通过torch.tensor([]),torch.zeros()等函数返回的对象都是类Tensor

（2）Tensor.backward() 到底干了什么?

先来看有数据的自变量$x$:

当我们在使用torch.tensor()对 自变量$x$ 进行构建的时候，曾经对参数进行设置为True，意思就相当于说，这个Tensor类保留了一个盛放自己导数值的单位tensor。

我们可以这样抽象理解：
这个表示自变量$x$的Tensor类具有两个单位tensor，

• 一个是主体的单位tensor：用于存放的是实实在在的这个自变量$x$的数值
• 另外一个是辅助的单位tensor：用于存放的是这个自变量$x$被求导之后的导函数值

当我们通过一些正常手段（例如使用Tensor类的函数）进行操作的时候都是操作在主体那个单位tensor上，剩下那个辅助的单位tensor，我们可以通过来访问那个辅助的单位tensor。

如果自变量$x$不经过导数计算，是不会有数据的，你访问得到是None。
所以所做的就是把导数值存放在里面。

需要注意的是不会自动清零的，他只会不断把新得到的数值累加到旧的数值上面，这就需要我们利用来给他清零（后面会有更详细的说明）。

那问题来了，也没见f.backward()传什么参数呀？那它是怎样做到的呢？

再来看有数据的因变量$f$

不知道你观察到没有，我这里和上面形容 x 和 f 都使用了“有数据”这个词语，因为无论是$x$还是$f$，他们的type()出来都是一个Tensor类，他们在首次出现在代码的时候都是有数据的。自变量x的数据来自于我们构建的时候的赋值，而$f$的数据在我们使用就确定了，而这也确定了$x$和$f$作为Tensor类的不同性，因为$f$是根据来自$x$的数据经过函数运算得到的。

输出$f$Tensor类会发现它的抽象数据结构如下：

• 一个是主体的单位tensor：用于存放的是实实在在的这个因变量$f$的数值
• grad_fn：用于存放的是一个Function类，记录了主体的单位tensor的来源的计算历史

grad_fn存放的是计算历史，这就能理解为什么能够求导了而且能够把结果直接操作到上了。

实际上，你会发现每一个Tensor类都能执行backward()函数，假如我们直接对自变量xTensor=[R]进行backward()，我们可以看到=[1]，就相当于对它自己常数进行求导$R^{{}^{\prime }}=1$

执行了backward()之后，不会对主体的单位tensor数值和自身的grad属性发生任何修改，$f$和$x$自身的backward意义不同，我们是通过x$\to$f，既然他有上一级的Tensor，就会把backward()的结果存放在上一级的Tensor类的grad里面。由于x是被我们直接制造出来的root Tensor，x.backward()的结果存在自己的grad里面。

pytoch构建的计算图是动态图，为了节约内存，所以每次一轮迭代完也即是进行了一次backward函数计算之后计算图就被在内存释放，因此如果你需要多次backward只需要在第一次反向传播时候添加一个标识，让计算图不被立即释放。

我们对上面的代码进行改写：

输出：

（1）zero_grad() 到底干了什么？

我们前文提到过Tensor类的grad数值只会在原有基础上增加，自己是不会覆盖的，所以我们每计算一次就应该清零。实际上，zero_grad()做的就是一个清理工作。
如果我们把换成，会发现得到一样的输出结果。

（2）step()函数到底干了什么？

首先，我们必须明白优化器是干什么的？现在我们有一个函数，我们现在需要到达一个谷点，也就是我们需要知道当函数在谷点的时候，自变量x到底等于多少，但是我们只能一个个点去尝试，所以我们必须要让梯度下降，也就是不断迭代x，每一次更换一次x的值，来促使梯度的值不断变小。

我们可以看回我们最基本的那个梯度下降算法：
$${\theta }_j:={\theta }_j?\alpha \frac{?J({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n)}{?{\theta }_j}$$
而这个$\theta$正是我们损失函数的自变量，所以我们在运算step()的时是参考了，也就是的结果，这也就是为啥backward会先执行，再执行step。
那他参考这个grad是在哪里得到的呢？
我们在最开始初始化的时候就已经把自变量x托管给optim类了，无论是我们自己编写的函数，还是已经封装好的损失函数。也就是说我们的optim类只需要损失函数的自变量即可。
我们自己的函数使用优化器：

封装的损失函数使用优化器：

我们已经知道，对于损失函数而言，weights和bias就是他的自变量，所以这里用weights和bias来初始化优化器就能说得通了。

反正记住这样一点：所有的优化都是围绕损失函数来转的，我们想要损失降到最小，我们想要损失函数最小的时候的那个自变量的值，就是我们需要的权值。整个训练的过程就是在求权值的过程。
完整的逻辑过程：

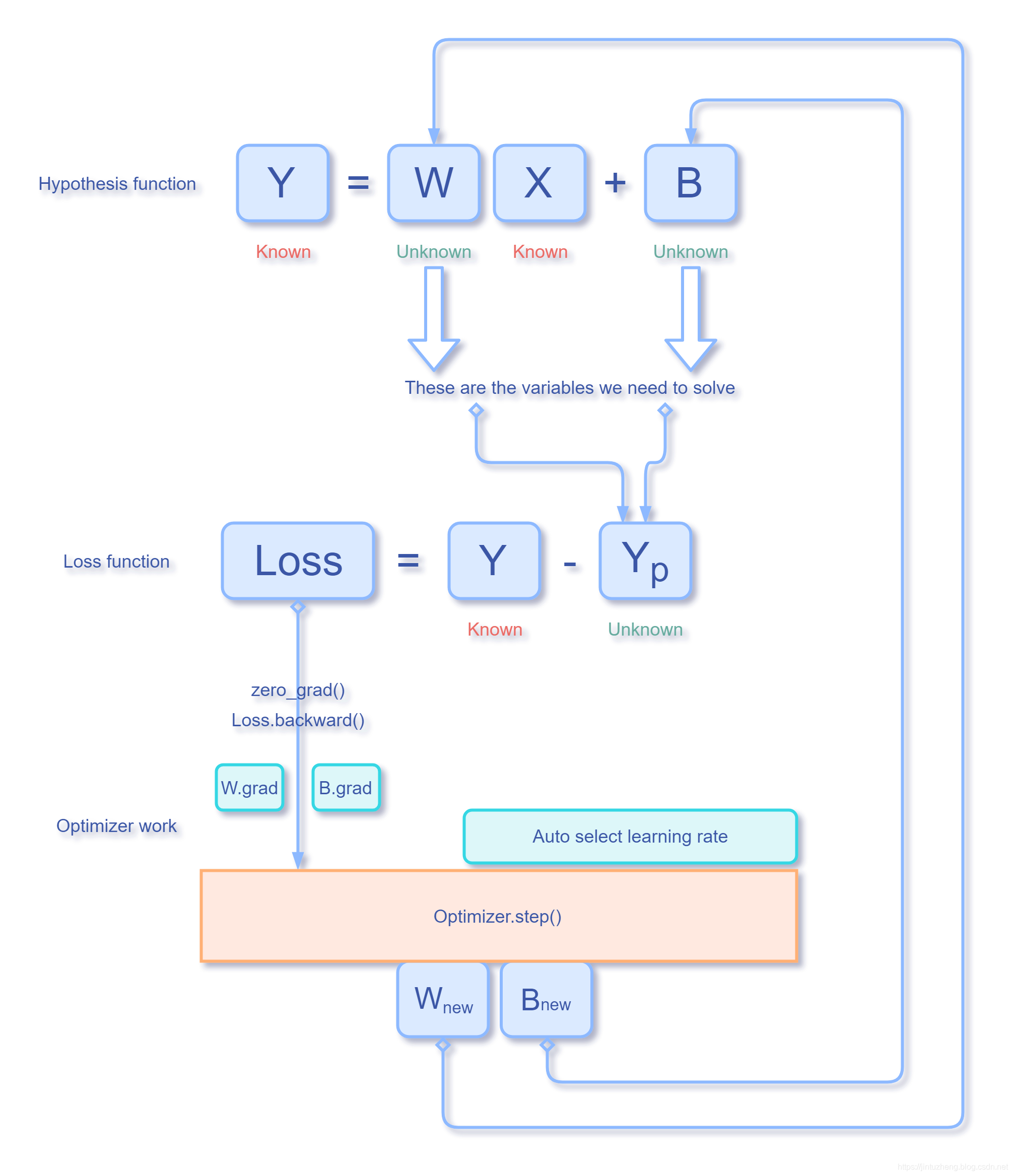
至此，我们给最开始的疑问代码打上注释：